What is the Hardy-Weinberg principle?
The Hardy-Weinberg principle, also referred to as the Hardy-Weinberg equilibrium, is a set of 5 assumptions which when satisfied can enable the determination of allele and genotype frequencies of a population. These frequencies will also remain constant for future generations. The principle was discovered by Godrey Hardy and Wilhelm Weinberg in 1908, based on Gregor Mendel’s Law of Segregation. To estimate the frequency of alleles and genotypes of a certain population, there is two simple formula that can be used.
The assumptions of the Hardy-Weinberg principle
There are 5 assumptions that are made when using the Hardy-Weinberg equations. These are:
- No natural selection: There are no evolutionary pressures which may favour a particular allele.
- Random mating: Each individual in a population mates randomly so that mating with an individual carrying a particular allele is not favoured.
- No mutations: There are no DNA mutations occurring for the alleles which may affect their function.
- A closed population: Individuals within the population do not leave and new individuals are not introduced to the population.
- Large population size: The population is considered large enough, at best infinite, so that major changes in allele frequencies do not cause a genetic drift.
If any of these assumptions are not satisfied, then the principle cannot be applied.
Determining the allele frequency
The first Hardy-Weinberg equation (p + q = 1) concerns estimating the frequency of alleles in a population. Each gene usually has two alleles (diploid organism), one from each parent. These alleles are denoted as the dominant (A) and recessive (a) forms. These are represented as ‘p‘ and ‘q‘ is the equation below.
In a population, the combined frequency of both the alleles must equal 1 (100%).
 Therefore, if the frequency of one allele is known, it is possible to calculate the frequency of the other allele simply by rearranging the equation.
Therefore, if the frequency of one allele is known, it is possible to calculate the frequency of the other allele simply by rearranging the equation.
Example
In a population, there are two alleles for ear shape: having detached lobes (dominant, A) or having attached lobes (recessive, a). Determine the allele frequency of the recessive allele ‘a’ (attached lobes) given the frequency of the dominant allele ‘A’ (attached lobes) is 73%.
1. To figure this out we first need to fill in what we know into the Hardy-Weinberg equation, i.e. the allele ‘A‘ (p in the equation) frequency is 73% (which is the same as 0.73).
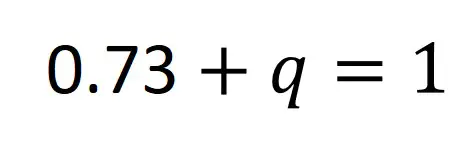 2. Next, rearrange the formula to determine the value of q (the recessive allele frequency). So this would give: q = 1 – 0.73.
2. Next, rearrange the formula to determine the value of q (the recessive allele frequency). So this would give: q = 1 – 0.73.
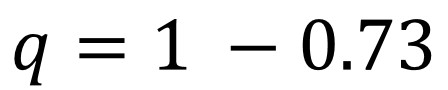 3. Calculating this would mean: q = 0.27 (27%). So, 27% of the population will have the allele for attached earlobes.
3. Calculating this would mean: q = 0.27 (27%). So, 27% of the population will have the allele for attached earlobes.
The recessive allele frequency is 27%.
Determining the genotype frequencies
The Hardy-Weinberg equation used to determine genotype frequencies is: p2 + 2pq + q2 = 1.
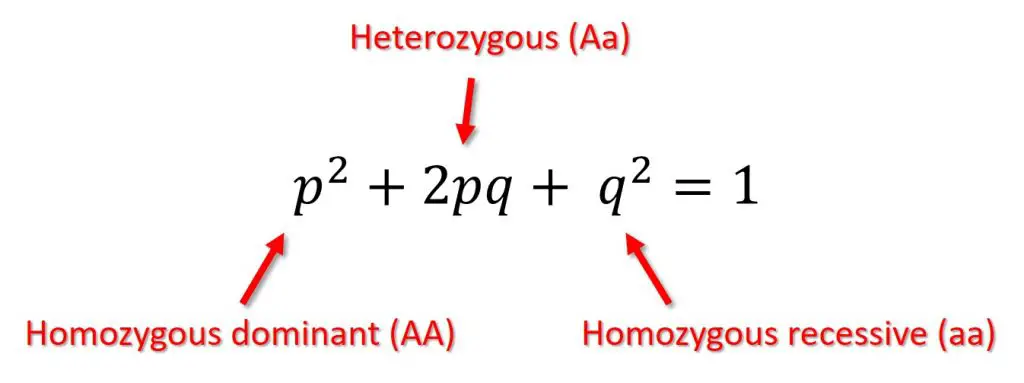 Where ‘p2‘ represents the frequency of the homozygous dominant genotype (AA), ‘2pq‘ the frequency of the heterozygous genotype (Aa) and ‘q2‘ the frequency of the homozygous recessive genotype (aa). The sum of these three genotypes must equal 1 (100%).
Where ‘p2‘ represents the frequency of the homozygous dominant genotype (AA), ‘2pq‘ the frequency of the heterozygous genotype (Aa) and ‘q2‘ the frequency of the homozygous recessive genotype (aa). The sum of these three genotypes must equal 1 (100%).
Again, if one genotype frequency is known, it is possible to use the Hardy-Weinberg equations to work out the others.
Example
Let’s use the same example above regarding earlobes (detached lobes and attached lobes). Determine the genotype frequency of the homozygous dominant (AA) allele for having detached earlobes given the frequency of the attached earlobe (aa) phenotype is 6%.
1. By looking at the question, we are asked to calculate (AA), so ‘p2‘ in the Hardy-Weinberg equation, given the frequency of aa (‘q2‘ in the equation) is 6% (we will work in decimals from this point, so this would be 0.06). Since ‘q2‘ equals 0.06, we can work out what ‘q‘ is by square-rooting 0.06. Doing this gives 0.245.
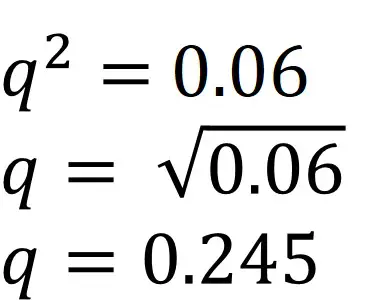 2. Since we now know the allele frequency of the recessive allele (q), we can use the first Hardy-Weinberg equation above (p + q = 1) to work out the allele frequency for the dominant allele (p).
2. Since we now know the allele frequency of the recessive allele (q), we can use the first Hardy-Weinberg equation above (p + q = 1) to work out the allele frequency for the dominant allele (p).
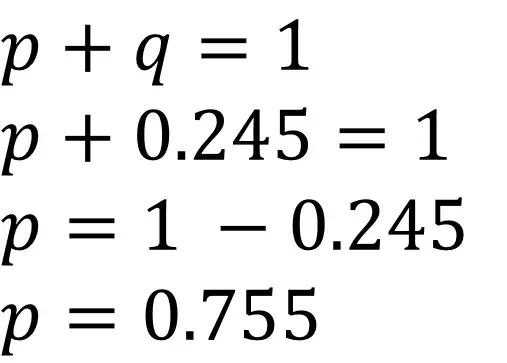 3. We now know what p is (0.755). To calculate the genotype frequency of the homozygous dominant genotype, we simply need to square the value of p. Doing this would give 0.57. So, 57% of the population are homozygous dominant (AA). This would be the answer to our question.
3. We now know what p is (0.755). To calculate the genotype frequency of the homozygous dominant genotype, we simply need to square the value of p. Doing this would give 0.57. So, 57% of the population are homozygous dominant (AA). This would be the answer to our question.
4. If you wanted to go one step further and work out the frequency of the heterozygous genotype (Aa), so ‘2pq‘ in the Hardy-Weinberg equation, you can do. Since we know the value of ‘p‘ (0.755) and ‘q‘ (0.245). All that is required is to multiply 2 by 0.755 and by 0.245. Doing this will give 0.37. So, 37% of the population will have the heterozygous genotype (Aa).
Notice, if you add all of the genotype frequencies together, this equals 1 (0.57 + 0.37 + 0.06 = 1).

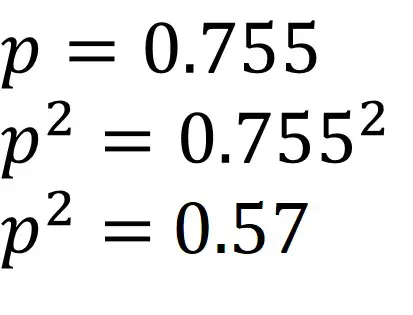



Thank youuu God bless you ?