In this guide, I will explain how to perform a Mann-Whitney U test in GraphPad Prism. I will also show you how to interpret and report the results.
Assumptions of a Mann-Whitney U test
Before performing the test, it is important to check that your data satisfies the assumptions of a Mann-Whitney U test. The assumptions are:
- The variables of interest contain continuous or ordinal data.
- There should be two groups of data present.
- Each data point should be independent of each other.
- The distribution and shape of the data in the two groups should be similar.
Setting up the GraphPad sheet
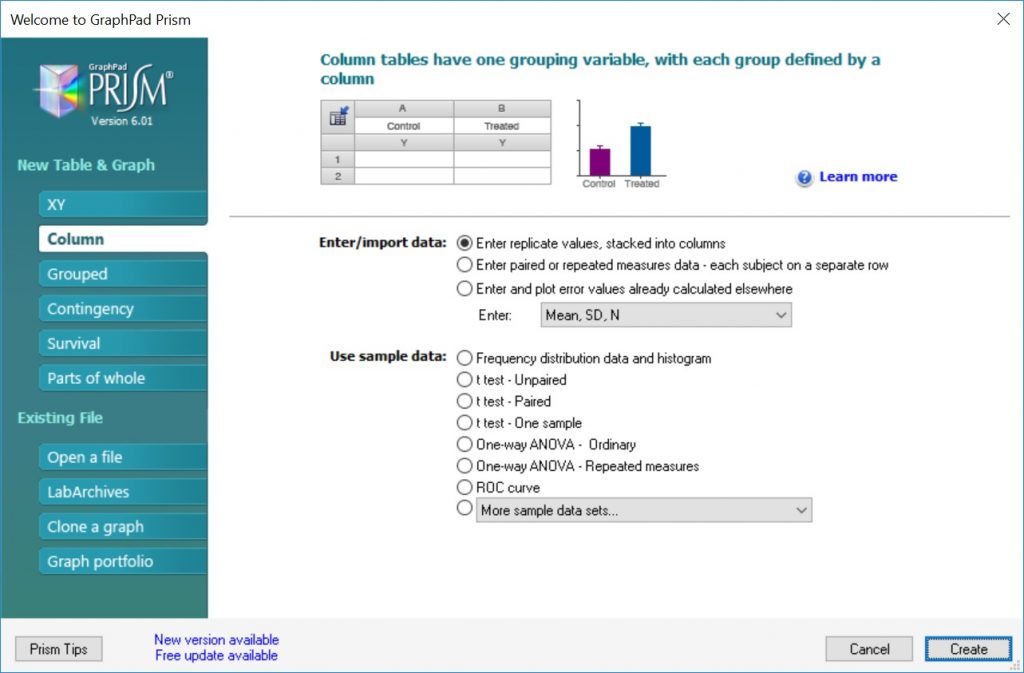
To perform a Mann-Whitney U test in GraphPad Prism you will need to enter two groups of data into separate columns. Upon opening GraphPad Prism, select the ‘Column’ type for the ‘New Table & Graph’ option. Then select ‘Enter replicate values, stacked into columns’ as the ‘Enter/import data’ choice.
Alternatively, you can go to ‘File > New > New Data Table & Graph …’.
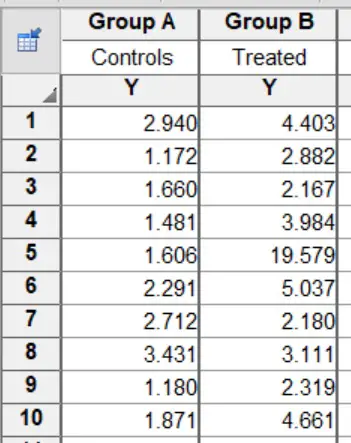
Example dataset
I will use a theoretical example of comparing the concentrations of a certain protein between a control and treated group of individuals. In total, I have 20 data points for each group. Each group’s data is separated into different columns.
The null hypothesis for this example will be:
“There is no difference in protein levels between the control and treated group”.
And the alternative hypothesis will be:
“There is a difference in protein levels between the control and treated group”.
Performing the test
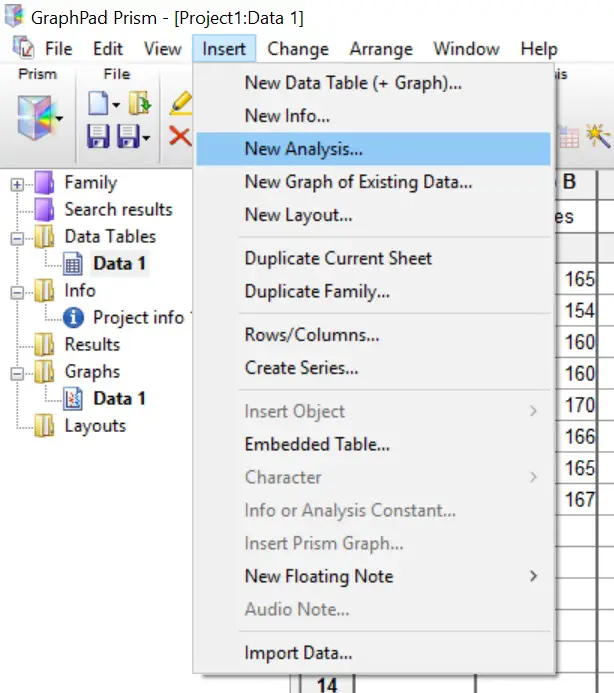
- To perform a Mann-Whitney U test in GraphPad Prism, first, go to ‘Insert > New Analysis …’.
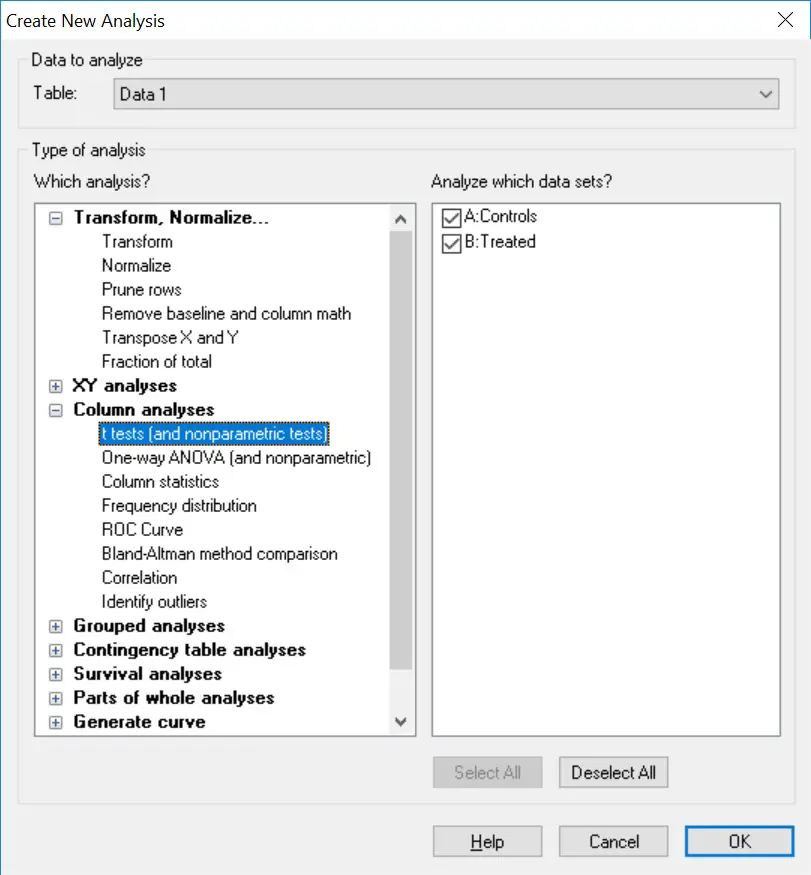
2. This will open a new window. Here you need to tell GraphPad which test to perform. Select the ‘t-tests (and nonparametric tests)’ analysis and make sure the two datasets are ticked on the right window. Click the ‘OK’ button.
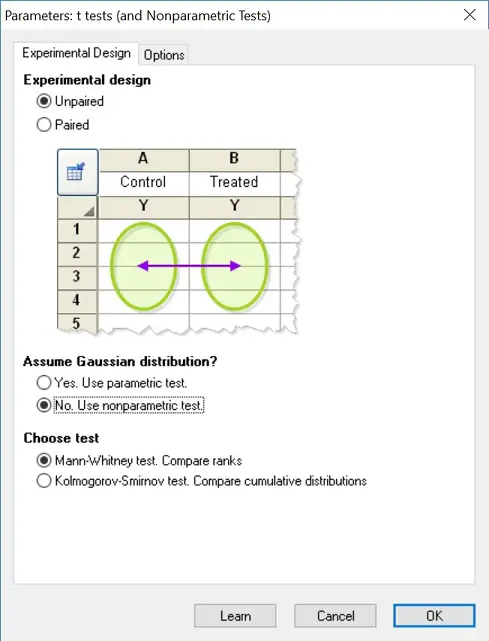
3. The next window will ask you to specify which test to perform. In this case, select the ‘unpaired’ option, under the ‘Experimental design‘ header. Next, select ‘No. Use nonparametric test’ under the ‘Assume Gaussian distribution’ header below. Finally, ensure the ‘Mann-Whitney test. Compare ranks‘ is selected under the ‘Choose test‘ header.
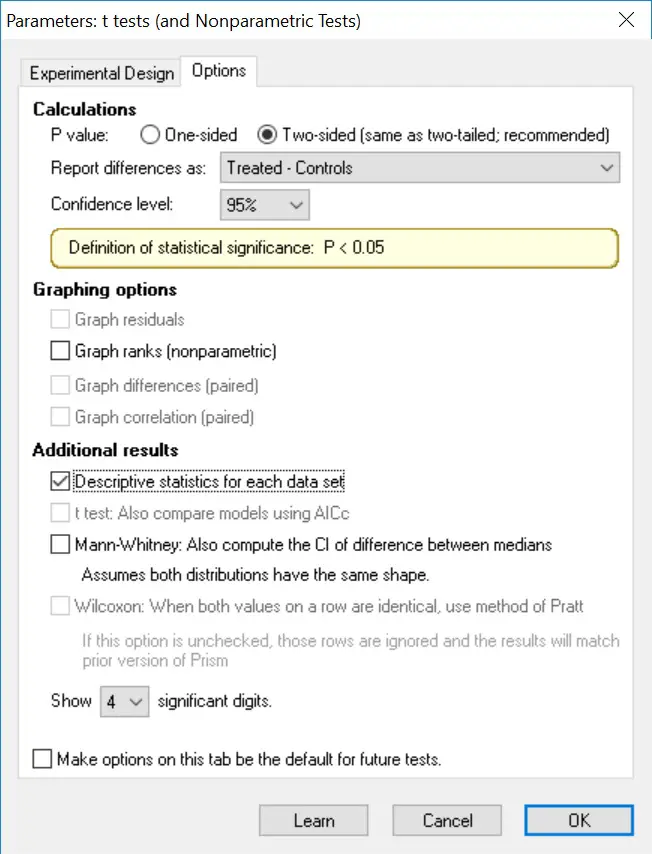
4. If you want to change any other settings, such as the confidence level, go to the ‘Options’ tab. For our purpose, we are going to leave everything in the default settings but will select ‘Descriptive statistics for each data set’ so GraphPad will produce the mean and standard deviation for each group. Click ‘OK’ to perform the test.
Output
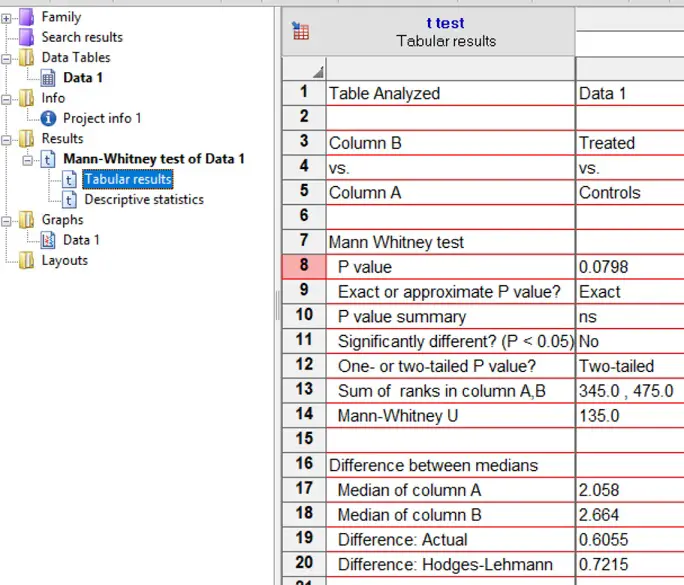
The great thing about GraphPad Prism for statistical testing is that the output is very user-friendly and self-explanatory. All you need to do is to refer to the ‘Tabular results’ sheet of the ‘Mann-Whitney test of Data 1‘ option on the left-hand side.
Focus on the output under the Mann Whitney test header. Each output is as follows:
- P value – The P value (of course!).
- Exact or approximate P value – Whether the P value was approximated or is exact.
- P value summary – A summary of the p-value as represented by asterisks. These are useful to signify the level of significance on graphs, for example.
- Significantly different? (P<0.05) – A straight yes or no answer to was there any significance.
- One- or two-tailed P value? – Whether a one- or two-tailed test was performed.
- Sum of ranks in column A,B – The sum of ranks for the two groups in the test.
- Mann-Whitney U – The U statistic.
Since we also selected the descriptive statistics to be reported, you can also find further information about each dataset in the test in the ‘Descriptive statistics‘ results sheet. This will be useful when writing the results since we need the median, 25th percentile and 75th percentile values.
Interpretation
By looking at the ‘Significantly different? (P<0.05)’ output, a ‘No’ is given which essentially means that our results are not significantly different from each other. The exact P value is given next to ‘P value’. In this case, a P value of 0.0798 is obviously larger than our level of significance threshold of 0.05.
Therefore, we accept the null hypothesis and reject the alternative hypothesis.
Reporting
If we were to report the results of this test in a paper, for example, we could write the following summary.
This includes the median, 25th percentile and 75th percentile (this information can be found in the ‘Descriptive statistics’ sheet) for each group, as well as the U value and the P value.
GraphPad Prism version used: 6