What is the coefficient of variation?
The coefficient of variation (CV) is a measure of precision from repeated measures. Within the lab, it is mainly used to determine how reliable assays are by determining the ratio of the standard deviation to the mean. The CV is the expressed as a percentage to easily determine the variation of the assay.
In terms of the CV for assays in the labs, there are two types: intra- and inter-assay CV.
Intra-assay CV is the variation of the sample measurement in the same run. For example, measuring a sample in duplicate or triplicate on the same plate. Intra-assay CV values should ideally be lower than 10%.
Inter-assay CV is the variation of the sample measurement on different runs. For example, measuring a sample on one plate and the same sample on a separate plate. Inter-assay CV values should ideally be less than 15%.
Usually the intra-assay CV value is lower than the inter-assay CV because the variation between runs is higher, than on the same run.
How to calculate the CV
To calculate the CV, you need to know the mean and the standard deviation for a series of measures. You then use the following equation:
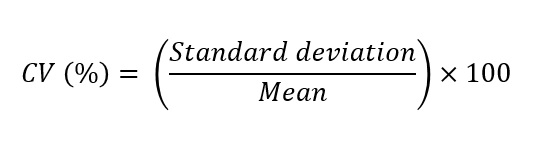 If you are using Microsoft Excel to work this out, you can use the following Excel formula. Just chane ‘Values’ to your number series of interest:
If you are using Microsoft Excel to work this out, you can use the following Excel formula. Just chane ‘Values’ to your number series of interest:
=(STDEV(Values)/AVERAGE(Values))*100
Example of using the CV
Let’s go through an example to understand the calculation better.
Imagine we have just performed an enzyme linked immunosorbent assay (ELISA) to calculate the concentration of protein X from the same plasma sample. We measured the same sample three times on a plate and on three different plates (Plates 1, 2 and 3). Here is our data:
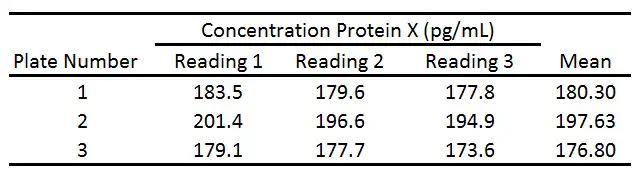
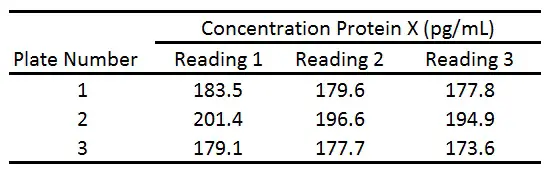 First, calculate the mean (average) between the readings 1-3 on each plate:
First, calculate the mean (average) between the readings 1-3 on each plate:
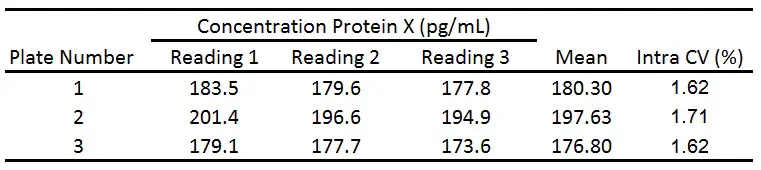
 We then use the CV formula above in Excel to calculate the intra-assay CV for each plate. This is the variation of measurements from the same plate (between readings 1, 2 and 3):
We then use the CV formula above in Excel to calculate the intra-assay CV for each plate. This is the variation of measurements from the same plate (between readings 1, 2 and 3):
 Finally, we can work out the inter-assay CV between the mean values from the three plates. This is an indication for the variation for the same readings on different plates:
Finally, we can work out the inter-assay CV between the mean values from the three plates. This is an indication for the variation for the same readings on different plates:
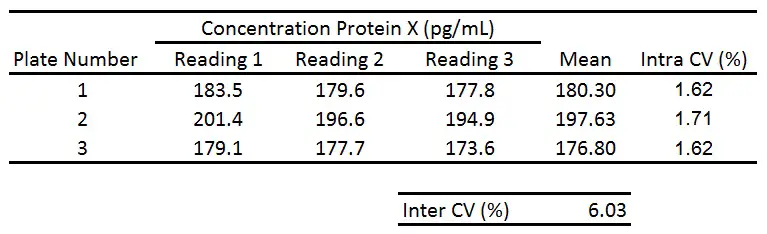 As you can see, the intra-assay CV is much lower than the inter-assay CV. Since the intra- and inter-assay CVs are less than 10% and 15%, respectively, this indicates a low amount of variation between measurements.
As you can see, the intra-assay CV is much lower than the inter-assay CV. Since the intra- and inter-assay CVs are less than 10% and 15%, respectively, this indicates a low amount of variation between measurements.




Hi Steven,
There seems to be confusion in the field about the nomenclature for CV and how it is expressed in a formulas. Would you look at my example below and give me your comments/ feedback?
I think we would agree that by definition CV is the standard deviation divided by the mean and that and that for precision we usually express it as a percentage, however, it could also be expressed as a ratio. This is shown with the following example:
If SD=6, mean =24, and CV =25% we can write:
CV=6/24
CV=0.25
CV= 0.25 x 100%
CV= 25%
The formula is CV= SD/mean x 100% or CV = SD/mean
However, in reports instead of writing CV=25%, I often see %CV = 25% and the formula for coefficient of variation incorrectly written as:
%CV = SD/mean x 100 or %CV =SD/mean x 100%
I believe %CV has been incorrectly adopted to indicate that the coefficient of variation is expressed as a % (for example as a header in a table to indicate that the list of precision values in the table are percentages). In other words, %CV was adopted as the nomenclature to indicate that precision values are CV values written as percentages. The problem with this is that by definition CV is a percentage or a ratio.
To get around this, I write the header as “CV (%)” just as I would write “concentration (mg/mL)” or volume (L).
I assume you are doing the same here because you are creating a formula that works in Excel.
CV(%) = SD/mean x 100
In other words, the correct formula for CV= SD/mean x 100% but since you are calculating with Excel as a percentage you use the formula CV(%) =SD/mean x 100.
Thanks, Nick
Hi Nick,
Many thanks for your comment.
Yes, I completely agree with you. I think %CV and CV(%) is often used interchangeably. I too would use CV(%) for my headers in tables to denote the output as being a percentage. Without the 100 the equation the output would indeed be a ratio, with 1 referring to 100%.
Best wishes,
Steven