How To Perform The Delta-Delta Ct Method

What is the delta-delta Ct method?

The delta-delta Ct method, also known as the 2–∆∆Ct method, is a simple formula used in order to calculate the relative fold gene expression of samples when performing real-time polymerase chain reaction (also known as qPCR). The method was devised by Kenneth Livak and Thomas Schmittgen in 2001 and has been cited over 61,000 times.

Mastering qPCR

Further video tutorials on qPCR data analysis can be found in our Mastering qPCR course
>>Use code 20QPCR to get 20% off<<

The FREE Microsoft Excel template

We have created a FREE Excel template which contains all of the formula described in this article below. Use this to practise and get the hang of the calculations. Everything is done for you, all that is required is the Ct values!

If you would like to download this, simply click here.

Understanding the delta-delta Ct method formula

It is worthwhile understanding what the delta-delta Ct formula means before diving straight into the calculations.

The overall formula to calculate the relative fold gene expression level can be presented as:

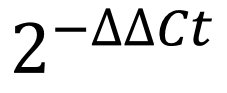2 delta delta Ct formulaThis looks like a scary mathematical formula when in actual fact, it isn’t. Let’s break the formula down into easier to understand chunks.

Firstly, Ct stands for the cycle threshold (Ct) of your sample. This is given after the qPCR reaction by the qPCR machine. Simply, it is the cycle number where the fluorescence generated by the PCR produce is distinguishable from the background noise.

The symbol ∆ refers to delta. Delta is a mathematical term used to describe the difference between two numbers. So it is useful to use when summarising long formulas.

So, let’s take a look to see what the ∆∆Ct part of the equation means:

∆∆Ct = ∆Ct (treated sample) – ∆Ct (untreated sample)

Essentially, ∆∆Ct is the difference between the ∆Ct values of the treated/experimental sample and the untreated/control sample. But what does ∆Ct refer to?

Let’s take a look:

∆Ct = Ct (gene of interest) – Ct (housekeeping gene)

Basically, ∆Ct is the difference in Ct values for your gene of interest and your housekeeping gene for a given sample. This is to essentially normalise the gene of interest to a gene which is not affected by your experiment, hence the housekeeping gene-term.

Using the delta-delta Ct formula to calculate gene expression

To use the delta-delta Ct method, you require Ct values for your gene of interest and your housekeeping gene for both the treated and untreated samples. If you have more than one housekeeping gene, it may be worth checking out the guide on analysing qPCR data with numerous reference genes.

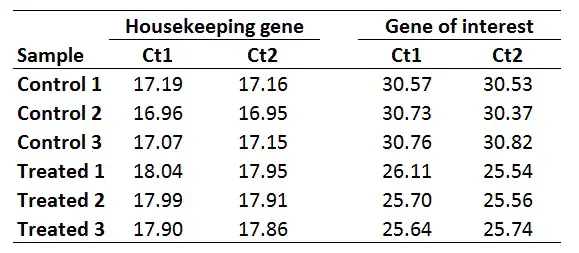Here is how to calculate the relative gene expression in 5 easy steps.

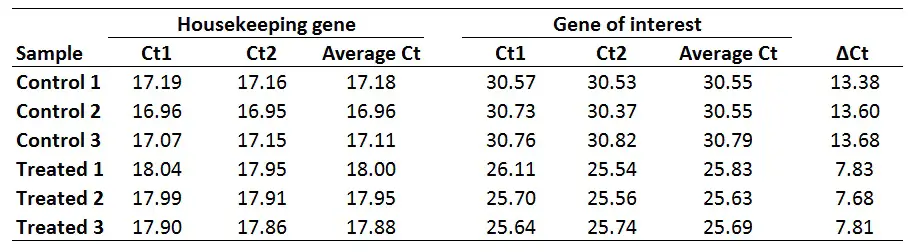
1. Average the Ct values for any technical replicates

The first step is to average the Ct values for the technical replicates of each sample. So, when performing the qPCR in duplicate or triplicate, for example, these values need to be averaged first. In the example below, each sample was run in duplicate (Ct1 and Ct2).

2. Calculate the delta Ct for each sample

The next step is to calculate delta Ct (∆Ct) for each sample by using the newly created average Ct values. The formula to calculate delta Ct is presented below.

∆Ct = Ct (gene of interest) – Ct (housekeeping gene)

For example, to calculate the ∆Ct for the ‘Control 1‘ sample:

∆Ct Control 1 = 30.55 – 17.18

 Calculate delta Ct

3. Select a calibrator/reference sample(s) to calculate delta delta Ct

The next step is to decide which sample, or group of samples, to use as a calibrator/reference when calculating the delta-delta Ct (∆∆Ct) values for all the samples. This is the part which confuses a lot of people. Basically, this all depends on your experiment set-up.

A common way of doing this is to just match the experimental samples and determine the relative gene expression ratios separately. This is all well and true for experiments that have matched pairs, such as the case in cell culture experiments. However, this is difficult when the two experimental groups vary in n numbers and do not have matched pairs.

Another way to select a calibrator/reference sample is to pick the sample with the highest Ct value, so the sample with the lowest gene expression. This way, all the results will be relative to this sample. Or, you could simply select just one of the control samples to act as the reference sample.

I personally average the ‘Average Ct’ values of the biological replicates of the control group to create a ‘Control average’. By doing so would mean that the results are presented relative to the control average Ct values.

Whichever sample, or group of samples, you use as your calibrator/reference is fine so long as this is consistent throughout the analyses and is reported in the results so it is clear. Remember, the results produced at the end are relative gene expression values.

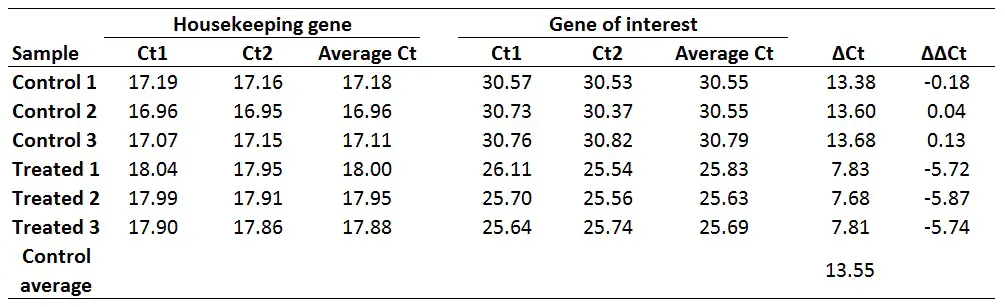
With this in mind, if we want to get ∆∆Ct values for every sample (including for each control sample), we first need to average the ∆Ct for the 3 control samples:

∆Ct Control average = (13.38 + 13.60 + 13.68)/3

Note, if the Ct values are variable, then it may be more appropriate to use the geometric mean instead of the arithmetic mean above. The geometric mean is more resistant to outliers, compared with the arithmetic mean. The geometric mean is used in the Vandesompele relative gene expression method for this reason.

For example, if the Ct values for my three control samples were 13.38, 13.60 and 15.80 instead, then this is a good reason to use the geometric mean rather than the arithmetic mean.

To use the geometric mean, firstly multiply the numbers together and then take the nth root of that value. The n is simply the number of observations in the formula, which is 3 in this example. So, using my latest example, this would be:

∆Ct Control geometric average = ∛(13.38 x 13.60 x 15.80)

4. Calculate delta delta Ct values for each sample

Now calculate the ∆∆Ct values for each sample. Remember, delta delta Ct values are relative to the untreated/control group in this example. The formula to calculate delta delta Ct is presented below.

∆∆Ct = ∆Ct (Sample) – ∆Ct (Control average)

For example, to calculate the ∆∆Ct for the Treated 1 sample:

∆∆Ct Treated 1 = 7.83 – 13.55

5. Calculate the fold gene expression values

Finally, to work out the fold gene expression we need to do 2 to the power of negative ∆∆Ct (i.e. the values which have just been created). The formula for this can be found below.

Fold gene expression = 2^-(∆∆Ct)

For example, to calculate the fold gene expression for the Treated 1 sample:

Fold gene expression = 2^-(-5.72)

Doing this would give a fold gene expression of 52.71 for the Treated 1 sample. Doing this for all of the samples will look like this:

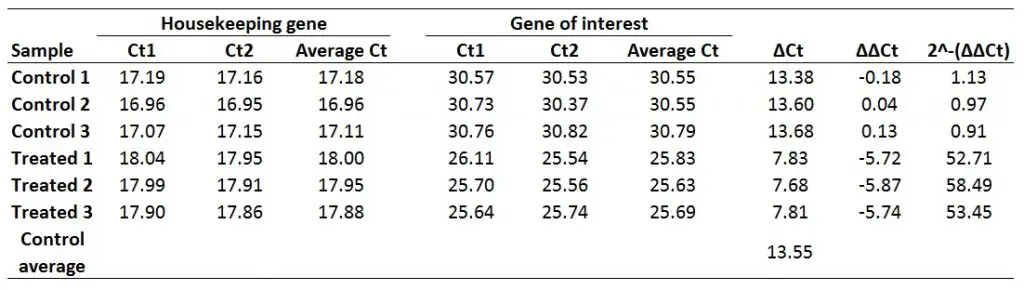And that is how you can use the delta-delta Ct method to work out the fold gene expression for your samples.

Statistical analysis

Just a point regarding statistical analysis of the gene expression values. It is always best to log transform the values (2^-∆∆Ct) before undertaking statistical analysis. This is because the untransformed gene expression values will most likely not be normally distributed and heavily skewed, especially in experiments where a strong stimulus is used. To do log transformations in Excel, simply use the log formula (=Log).

Then, the choice of statistical test will be dependent on your experimental set-up. If you are struggling to perform a particular test, refer to our selection of SPSS and GraphPad Prism tutorials.

RELATED ARTICLESMORE FROM AUTHOR

87 COMMENTS

  2. Dear Steven,
    Thank you very much for your explanation. I just wonder about the calculation you present and apply. Ct values represent an EXPONENT. Thus, when using exponents one leaves the real number and enters the logarithm world. Let’s assume a triplicate of 10, 100, and 1000. Real numbers: mean value is: 1110 : 3 = 370. Logarithm (log (not ld) to make it simple) – as you propose) (1 + 2 + 3) : 3 = 2 Thus, the mean value becomes 10 exp2 = 100. The mistake lies in calculating the mean as “plus” in a real number fashion but using logarithmic values.
    For practical use the error will be small/ neglectible when values are next to each other but not in other cases (as can be seen in my example with extreme values) and of course it is mathematically simply wrong.

    • Hi Andreas,
      Apologies this is a late reply and thanks very much for the feedback, I really appreciate it.
      I agree that the arithmetic mean may not be suitable for averaging exponent values that are far apart. A way around this would be to use the geometric mean instead, which is more resistant to outliers. I have reflected this point in the artice now. In fact, this is used in the Vandesompele method of relative gene expression analysis. Having said that, in my experience, my biological replicates have always been within a few Ct values of one another; this may be due to the cell models I use.
      Again, my averaging approach is just one way of selecting the calibrator. You could just choose one sample as the calibrator.
      Thanks,
      Steven

    • Hi Maryam,
      I recommend log-transforming the final gene expression values (ddCT). Then performing the normality tests on these values.
      I hope that helps.
      Steven

  6. thanks for this amazing explanation,
    my work is on relative gene expression for mRNA from bacteria before and after different treatments,
    my first question is the control here is the reference gene(that have CT(16.23) less than that of untreated sample (21.8)?)
    or to take the untreated sample as control but in this case i will have fold change equal 1 and the treated groups have lower gene expression(ct equals to 26, 27,…) that can’t be calculated by 2 -ddct method
    so what to do to be able to show the down regulation of the gene expression that occurs due to the treatment with antibiotics in my experiment,,,thanks in advance

  7. Hi Steven,
    Thank you so much for sharing that informative article.
    I have a same question as Yogesh. How can I calculate or analyze gene expression data without control group and just based on Housekeeping gene? I have three housekeeping gene. Is it possible to just perform delta ct to get the ratio and then run Anova test based on mean of delta ct and variance? or I have to do 2 to the power of the delta ct value to get the relative gene expression and then perform statistics on?
    Many thanks
    Shirin

    • Hi Shirin,
      I would advise using the same approach as I recommended to Yogesh. Or use the method for analysing with multiple reference genes. Pick any sample in your experiment as the ‘calibrator’ since you do not have a control group/sample. Go right to the end and then log-transform your data before statistical analyses.
      I hope that makes sense?
      Steven

      • Hi Steven,

        Thank you very much. your answer was clear. Just wanted to double check is it fine if I just chose one or two samples with low gene expression as a calibrator?

        Many thanks,
        Shirin

  8. Hi Steven,

    Thanks for your article.
    I have a question concerning the reference condition: my gene of interest is only expressed in my treated condition and not in my reference condition (Ct >40 or no value at all).
    How can I do to calculate my deltadelta Ct ? If I use values >40 cycles, I obtain results that are not “correct” biologically.

    • Hi Aurore,
      In your case, you could just describe your results; stating that the reference condition was too low expressed to be detected (i.e. Ct >40). It sounds like the difference between your reference and treated groups are quite large anyway so you don’t need to perform statistical analyses to show this.
      I hope that helps.
      Steven

  9. Thank you for sharing this. The gene of interest you used showed higher ct than the housekeeping gene, which I also observed in my previous experiments. But recently I did an qPCR which revealed a lower ct for my gene of interest in comparisson with the housekeeping (HMBS).My gene of interest is overexpressed in my samples (an oncogene in tumor), but I don’t know if that is suppose to happen. If I calculate the delta ct as ct [gene of interest] – ct [housekeeping gene] , I get a negative result. Is it correct to assume the delta ct would be just the difference between than, so it would be positive anyway? Is it the same for the delta delta ct formula (with negative results) if it’s a comparisson with the sample with lower expression?

    • Hi Ricardo,
      Usually your housekeeping gene should be strongly expressed (lower Ct value) compared with your gene of interest. But, in experiments where there is a strong stimulus then it is possible that the gene of interest can be more expressed. However, I would double-check your product, i.e. it is not primer-dimer (melt curve analysis or running product on a gel will answer this – if SYBR green assays are used), just to confirm there is nothing strange going on in the reaction.
      The equations stay the same regardless of the Ct values, so the delta Ct is always the Ct[gene of interest]-Ct[housekeeping gene] – if that is what your last question refers to?
      Thanks,
      Steven

  10. it was very useful! Thank you!

    To calculate the standard deviation/error for error bars on the graph, which values would you use?

    • Hi Maheshika,
      Many thanks for the message.
      For this I would calculate the standard error of the gene expression values at the end. You would need numerous biological replicates per group to be able to do this (i.e. repeat your experiment multiple times).
      I hope that helps.
      Steven

  11. Hello Dr. Bradburn,

    Thanks for nice description on how to calculate ddCt. My question is how to calculate ddCt if you don’t have “Control” group? In my assay I have gene of interest and house keeping gene, is it still possible to calculate ddCt?

    • Hi Yogesh,
      Many thanks for your kind comment.
      Sure it is possible. If you just have a group of samples instead of a control group you can just select 1 sample as the calibrator (control) sample. Then everything will be relative to this.
      I hope that makes sense.
      Steven

  12. Hello Steven,
    I used to do the analysis the same way you do, normalizing on the average of the controls. For the significance I usually perform the Pairwise Wilcoxon Rank Sum Tests.
    However, I am now analyzing samples in which I have a lot of variability between biological replicates. If I normalize each replicate on it internal control this variability is greatly reduced. However, doing so the sample “control” becomes simply 1. What kind of non parametric test should I do to test whether the ddCT of my treatments are significantly different than 0? The Pairwise Wilcoxon Rank Sum Tests works with pair and I lose the control since it becomes = 1 in all the samples. Can I perform the one-sample Wilcoxon signed rank test with null hypothesis = 1 for each gene and then adjust for multiple comparison?
    Thanks,
    Marco

    • Hi Marco,
      Many thanks for your message.
      I recommend log-transforming your gene expression data before performing statistical analyses. Either using the base of 10 or 2. This should help out with the normality of the data too. After doing this, would your data still be skewed or not normal? If it’s comparing 2 groups then either an independent student t-test or a Mann-Whitney U test should do the trick. Unless I am missing something? When selecting your calibrator sample you can select just one of the ‘controls’ that way only 1 sample in the experiment will have a 2^-ddCT of 1.
      Thanks,
      Steven

  13. Hi Steven,

    Really informative article. Your data is examining the changes in expression for control group and treated in GOI and HKG . I wanted to examine the effects that a non-coding variant in an enhancer sequence in one sample (called experimental) would have on gene expression in comparison to 3 healthy controls (control 1,2,3) in the GOI and GAPDH

    My 2^-ΔΔCt values for control 1, 2, 3, are 0.687, 0.723 and 0.718. This would indicate that there is down regulation in the experimental sample in comparison to the 3 controls. My question is can statistical analysis be performed using the log transformation of these numbers ?

    Fintan

    • Hi Fintan,
      Many thanks for your feedback!
      It would be hard to perfrom statistical analysis if you have 1 sample in one group (experimental) and 3 samples in the other group (control). Ideally, you need more biological replicates, especially in your experimental group. Is there any way you can repeat the experiment?
      Also regarding your set-up, which sample did you use as your ‘calibrator’ in the equation?
      Many thanks,
      Steven

  14. Following from my last response, how would I explain fold change when looking at the log(2^-ddCt) values? For example, the fold change for a sample was originally 0.7 fold increase (when the control 2^-ddCt = 1) but now the sample log value is 0.2 compared to the untreated log value of 0 – would I say it has 0.2 fold increase?

    Thank you

  15. Hi Dr Bradburn, thanks for ur good explanations. When we test samples in duplicate, and between the duplicates is more than 1cycles differences, what would be the problem?
    And how can I find out that the expression of my treated have enough change? What ddtc should I have that I could say my drug is infected?

    • Hi Fatemeh,
      If your technical replicates are >1 Ct apart then this could be errors in pipetting and handling. Try pipetting larger sample volumes into the reaction (eg 3 uL, as opposed to 0.5 uL). This will make it a lot easier.
      For your second question, there is no magic answer. You will need to perform statistical tests (eg T tests) to determine any statistically signififcant differences between groups.
      Many thanks,
      Steven

  16. Hi Steven..thank you for your great explanation. I am planning to do comparison of miRNA expression before and after treatment. in this case, is DDCT applicable? do I need a control group or the “before” treatment group will serve as control group it self?
    I am a bit confused since many paper about miRNA expression mentioned only delta CT, not delta delta CT method..
    Thanks

    • Hi Grace,
      You can use the DDCt method for miRNA only if you have a reference miRNA gene in your experiment. Many miRNA screening assays include these. You also need a control or before group, to act as the comparator. Alternatively, the delta Ct method is usually applied to miRNA analysis if there are no reference genes or specific experimental groups.
      I hope that helps.
      Best wishes,
      Steven

  17. Hi Steven,

    How would you obtain P-values and run statistical analysis even if you log the 2^-deltadeltaCt values as there is no 2^-deltadeltaCt value for the untreated alone? Really confused about how I can analyse the data besides obtaining 2^-deltadeltaCt and showing it in a graph.

    Thank you 🙂

    • Hi Karolina,
      Many thanks for your message.
      I advise log-transforming the 2^-DDCt values then performing your statistical analyses on these values. You control group will have an average value of 0, since the log of 1 is 0.
      I hope that makes sense.
      Best wishes,
      Steven

      • Thank you for your response! Would it be best to use the transformation data to display in a graph or is it possible to use the original values and indicate which values are significant based on the analyses from the transformed data?

        Thank you 🙂

        • Hi Karolina,
          You could do either. To save confusion I would plot and perform the statistical analyses using the transformed data.
          Best wishes,
          Steven

    • Hi Mona,
      Many thanks for your comment.
      What was the ddCt value for this sample (the step before the final 2^-ddct)?
      Thanks,
      Steven

  20. Hi Steven,

    I am just wondering how I would go about calculating standard error, or similarly a 95% confidence interval using the related standard deviations using this method.

    Thanks,

    Zach

  21. Hi Steven
    Thank you for a great text and explanation of a method.
    ı have three groups: malignant tumor- corresponding non-neoplastic tissue and another benign disease group
    I am wondering, Can ı use corresponding non-neoplastic tissues average delta CT value to calculate benign disease group delta delta CT value

    • Hi Gizem,

      Yes, you can use the non-neoplastic tissue group as the ‘calibrator sample/group’. When reporting the results, you will have to stress that the results are relative to the non-nepplastic group.

      I hope that makes sense,

      Steven

  23. thanks steven
    i see that, my question is can i use the final relative gene expression of alternative method as fold gene expression for my samples. i study on CNV changes.

  25. Thanks Steven for your reply.
    I want to calculate the plasmid copy number compared to a single gene on chromosome using Delta-Delta Ct method or any other relevant method.
    My plasmid size is 6179 bp and genome size is 7416678 bp. The above dilution series is pg/uL of DNA from 0.1 pg/uL upto 100000 pg/uL.
    thanks,
    Muhammad

  26. Dear Steven,
    Thank you so much for uploading this video which answered many questions.
    I want to determine the copy number of a vector compared to genome and run some qPCR as follows,
    each dilution was run with 3 replicas and Mean Cp values are given below:
    Plasmid 0.1 dilution Mean Cp value 32.24
    Plasmid 1 dilution Mean Cp value 30.73
    Plasmid 10 dilution Mean Cp value 27.89
    Plasmid 100 dilution Mean Cp value25.64
    Plasmid 1000 dilution Mean Cp value 22.02
    Plasmid 10000 dilution Mean Cp value 17.74
    Plasmid 100000 dilution Mean Cp value13.63

    Chromosome gene Mean Cp values:

    Chrm 0.1 dilution Mean Cp value 35.05
    Chrm 1 dilution Mean Cp value 33.75
    Chrm 10 dilution Mean Cp value 30.16
    Chrm 100 dilution Mean Cp value 28.04
    Chrm 1000 dilution Mean Cp value 24.35
    Chrm 10000 dilution Mean Cp value 20.03
    Chrm 100000 dilution Mean Cp value 15.95

    How can I use Delta-Delta cp method to determine plasmid copy number compared to chromosome gene which is single copy gene?

    Looking forward to hearing from you soon.

    Thanks,
    Muhammad

    • Hi Muhammad,
      Many thanks for your comment.
      Regarding your experiment, are you wanting to calculate the copy number (there are online calculators to do this, e.g. http://scienceprimer.com/copy-number-calculator-for-realtime-pcr – I am also in the process of making one for this site)? This requires entering the concentration and length (in base pairs) for the gene product. Or are you wanting to measure gene expression values via the Delta-Delta Ct method?
      Best wishes,
      Steven

      • Thanks Steven for your reply.
        I want to calculate the plasmid copy number compared to a single gene on chromosome using Delta-Delta Ct method or any other relevant method.
        My plasmid size is 6179 bp and genome size is 7416678 bp. The above dilution series is pg/uL of DNA from 0.1 pg/uL upto 100000 pg/uL.
        thanks,
        Muhammad

        • Hi Muhammad,
          Sorry for the late reply.
          I have very little experience in calculating plasmid copy numbers in the experiment you have described. Is the gene the same from the plasmid and the genome?
          The delta-delta Ct method is used as a comparative gene expression method. Another note is that the delta-delta Ct method requires a reference (housekeeping) gene. There is also a way to calculate absolute gene expression – through a similar way you have described whereby you perform a standard curve and use this to determine unknown samples. However, you do not have these unknown samples, just the standards. Is this correct?
          Thanks,
          Steven
          To calculate

  27. Hi Steven,
    thank you for a great text and explanation of a method.
    I have one doubt, maybe you could help: is it still ok to use the Delta Delta Ct method when my target gene primers Efficiency is 104% and my housekeeping gene primers have Efficiency of 93%?
    Thank you in advance!
    DM

    • Hi Danica
      Many thanks for your message.
      The delta-delta Ct method assumes your primer efficiencies between your target gene and housekeeping gene are the same (or roughtly the same). However, what would be even better in your case is to use the Pfaffl equation to account for the slight differences in primer efficiencies. Since you already have the primer efficiencies for each gene (which is great), you can do this easily enough.

      Here is my guide on how to do it:

      https://toptipbio.com/pfaffl-method-qpcr/

      Let me know if it doesn’t make sense and I will help.

      Best wishes,
      Steven

  28. Hi Steven,

    Thank you a lot for the great work!!! I am checking RNAi knockdown efficiency and I have 2 controls instead of one and 1 test. I designed the experiment where I have 3 technical replicates and 3 biological replicates. How do I select the calibrator/reference sample? You mentioned, “Another way to select a calibrator/reference sample is to pick the sample with the highest Ct value, so the sample with the lowest gene expression.”
    Sorry if this is confusing. Please advise me what to do since I have 2 controls.

    Thanks in advance!
    Kay

    • Hi Kay,
      Thanks for your message.
      Okay, so you have 2 control groups. Are you planning on statistically comparing all 3 groups to each other (control 1 v control 2, control 1 v test, control 2 v test)? If so, just select either one sample from one of the control groups (doesn’t matter which) or calculate the average delta Ct for one of the control groups (like I do in the example) and use this as the calibrator.
      Does that make sense?
      Thanks,
      Steven

  29. Hey Steven! Thank you for an amazing explanation, found it incredibly helpful. When using this method, some of the fold gene expression values calculated was really high (25, 76 etc.). Is this acceptable? What do these results mean? Is there a range that is acceptable?
    Thank you in advance!

    • Hi Kynesha,
      Many thanks for your comment. I am glad it helped you.
      So there is no general range that gene expression values will be – this is all dependent on your experiment and genes you are investigating. For example, in cell culture experiments you can stimulate cells and cause a huge increase in certain gene expression (sometimes in the thousands), so don’t worry about your results.
      What these results mean is that those samples are upregulated, compared to you calibrator sample(s), such as a control or untreated group.
      Does that make sense?
      Best wishes,
      Steven

  30. I would like to suscribe to top tip bio but the page does not say how expensive it is. I like the way you teach,

    • Hi Leticia,
      Many thanks for your comment. All of the content on this website is free. There will be some premium courses coming in the near future, containing a complete guide of qPCR and its analysis.
      To keep up to date with content and news, you can subscribe to our Facebook and Twitter pages, and find free video tutorials on out YouTube channel.
      Best wishes,
      Steven

  31. Hi Steve,

    Thank you for easy explanation. I have used this method but in my case i had only disease group and i used two explants as treated group and two explants from same sample as control group. In control group external stimulus was not applied. In this way i evaluated the effect of stimulus on fold expression change in patients. I wonder if i did it in a right way??? Any comments from you?

    • Hi Kanwal,
      Many thanks for your comment. Sure, that sounds fine the way you have done it. So you have untreated (control) and treated samples with a stimulus. Then the results will be relative to the untreated.
      Best wishes,
      Steven

  33. Dear Steven,
    Thanks for your very easy-to-follow explanation. I wonder how is the best way to calculate when one wants to compare 3(+) groups. In my case, I’m comparing control (A) x “diseased” (B)x “treated” (C)…definitely I could calculate the ddCt from B-A and C-A to compare both experimental groups to the control. But the how should I apply the statistical analysis? I mean: should I apply directly to the 2^(-ddCt) values? Would it be reasonable if i apply a linear statistical test (as all of the basic tests) to a base-2 fold-change data? Also: any suggestion of how to plot these data? As fold-changes in linear scale or log(2) scale?

    Thank you very much!

    • Hi Maria,
      Many thanks for your comment. Regarding the results, you could calculate all the group 2^(-ddCT) values relative to the control group, I think this would be the best option.
      For the statistics, you would use a one-way ANOVA on the 2^(-ddCT) values to detect differences between groups. If you want to plot the results, it depends on the values of 2^(-ddCT) in your groups. If there are large differences in values between groups, it may be best to present them on a log scale.
      I hope that answers your questions?
      Best wishes,
      Steven

  34. Dear Steven,

    I am wondering where in the analysis you can perform a outlier test on the data set. I have 3 groups (mice) with N=14, and used 1 group as control group to calculate the ddCT and 2-(ddCT).

    Is it Ok to use a Grubbs test? And should I use it on the ddCT/2-(ddCT) values?

    Thanks

    • Hi Elise,
      Certainly, you can perform an outlier test. The Grubbs test should be fine for you, and I would do this on the 2-(ddCT) values.
      Good luck with is!
      Best wishes,
      Steven

  35. Thank you for great note!
    I wonder about the case that control group sample doesn’t have any GOI.
    For example, control group are wild type mouse and experimental group are knock-in mouse (EGFP).
    In this case, control group GOI was not detect any RT-qPCR result using EGFP primer.
    However, control group housekeeping gene was have Cq value such as 20.
    Then, how I can calculate delta Cq value of control? Was Cq of EGFP regarded zero?

    • Hi Lora
      In your case, you could give the samples with no signal on qPCR a Cq value of 40 (or the maximum cycle number from your qPCR run). That is, if you still want a value for your control group to do statistics? Obviously the difference is so strong anyway. But this will give you something at least to plot on a graph if you so wish?
      Thanks
      Steven

  36. Dear Steve
    I am really thankful for your explanation, I have understood perfectly (at least to do it in excel), but I would like to know if you have ever working with circulating microRNA expression? Because, I am going to work with that and I want to know if it applies the same method.

    Thank you so much for your time.
    Larissa.

    • Hi Larissa,
      Many thanks for your comment. I personally haven’t done qPCR on miRNAs. But it will depend on your experiment set-up. If you have control and treated samples, with at least one housekeeping gene then I am sure you can use the delta-delta Ct method as described for mRNA.
      Best wishes,
      Steven

  37. Why did you average the control? when you do this then you have a fold change different from 1. I have read that there should not be standard deviation from the control group as you are showing in this example…

    • Hi Irene,
      Many thanks for your comment.
      I used the average control delta Ct since this will enable the calculation of 2^-(∆∆Ct) for all the samples, including the individual control samples.
      Other people just match the experimental samples and determine the relative gene expression ratios separately. This is all well and true for experiments that have matched pairs, however, this is difficult when the two experimental groups vary in n numbers and do not have matched pairs. Another way to select a calibrator/reference sample is to pick the sample with the highest Ct value, so the sample with the lowest gene expression. This way, all the results will be relative to this sample.

      If you want to get an overall average fold change of 1 for the control group, you can normailse the results. To do this you would make a new column and divide all of the gene expression values (2^-DDCt) for all the samples by the control group average 2^-DDCt. Then average these values for the controls and the treated. The control average should now be set to ‘1’.
      I hope that makes sense?
      Thanks
      Steven

  38. Hi Steven,
    Nice summary on delta delta Ct calculation.
    One question: Is one cell line treated in 3 different wells on the same day considered as n=3 for statistical analysis? Or do I have to treat the cells on 3 different days in order to add error bar?

    • Hi Jon,
      Many thanks for your comment!
      Ideally, it will be best to repeat the experiment on different days to be classed as true biological replicates. Since if you repeat it on the same day, obviously the variation will be lower, however, it is not an accurate representation of the amount of variation experienced.
      Refer to this recent paper in PLoS Biol by Lazic and colleagues which nicely sums this up (in the Cell Culture section).
      I hope that makes sense?
      Kind regards,
      Steven

    • Hi Kurt,
      Many thanks for your comment and apologies for the slow reply.
      To handle multiple reference genes, it is best to take the geometric mean of the housekeeping gene Ct values. Then use this value to create the delta Ct’s.
      I will shortly create an article on how to do this with more detail.
      I hope that helps.
      Best wishes,
      Steven

  40. Dear Dr. Steven,

    Thank you for the video.
    Can you please tell me how to tell that there is Up or down-regulation of the gene by using the Fold change value.
    Thank you.
    Regards
    Houda

    • Hi Houda,
      Many thanks for your comment.
      To understand if there is an up- or down-regulation of your genes in a comparison between controls and treated groups, you simply compare the gene expression values between the two groups. So if the average gene expression of the controls was 1.2 and the treated group was 2.6 this would mean that there is an upregulation of the gene in the treated group. Conversely, if the values were 1.2 in the control and 0.8 in the treated group, this would mean that there is a downregulation in the treated group.
      I hope that makes sense?
      Best wishes,
      Steven

        • Hi Nina,
          Many thanks for your comment, and sorry about the slow reply.
          When I say “fold gene expression values”, I am referring to the final 2^-(∆∆Ct) values.
          I hope that clears it up.
          Best wishes,
          Steven

          • Hi Steven,

            I am wondering how you get “fold gene expression values” for your control samples, since the way you get those values for your experimental samples is by comparing it to the control samples. What are you using to get the delta delta CT for your control values?

            Thanks,
            Alaina

          • Hi Alaina
            Thanks for your comment.
            This way described, I still get fold gene expression values for all the control samples (refer to the 2^-(∆∆Ct) column in the above table).
            To get delta delta Ct values for the control samples, I use the average delta Ct value from the control group (see the Control average row in the above table) to compare against.
            I hope that makes sense.
            Best wishes,
            Steven

  41. Dear Sir

    Thank you for your video

    I have some of my genes cannot express in the treated group. If I use the Average from one sample the result some time not logical but I got express for the housekeeping gene.

    for example, housekeeping gene values cq 28, 27, 29 but my treated group I got only one value 37 but cq value for other sample or replicate

    Ashwaq

    • Hi Ashwaq,
      Thanks for your comment!
      So you got a Cq value of 37 for the housekeeping gene in your treated group? It sounds like your housekeeping gene is expressed at such a low level in your treated group, compared to your controls. This would suggest that the experiment is having a significant influence on the expression of this gene, therefore I would not recommend using it as a housekeeping gene. A suitable housekeeping gene should have the same or very similar values between your control and treated groups. It may be worth trying out a panel of different housekeeping genes to see which ones are the best.
      I hope that helps.
      Best wishes,
      Steven

LEAVE A REPLY

Please enter your comment!
Please enter your name here