What is a one-sample t-test test?
A one-sample t-test is a statistical procedure used to determine if there is a significant difference between the sample mean and a known or estimated population mean.
Assumptions of a one-sample t-test
Before performing the test, it is important to check that your data satisfies the assumptions of the one-sample t-test. These are:
- The variable of interest contains continuous data (interval or ratio).
- Each data point should be independent of each other.
- There are no significant outliers present in the data.
- The variable of interest should be approximately normally distributed. Refer to our guide on how to test for normality in SPSS.
Example data
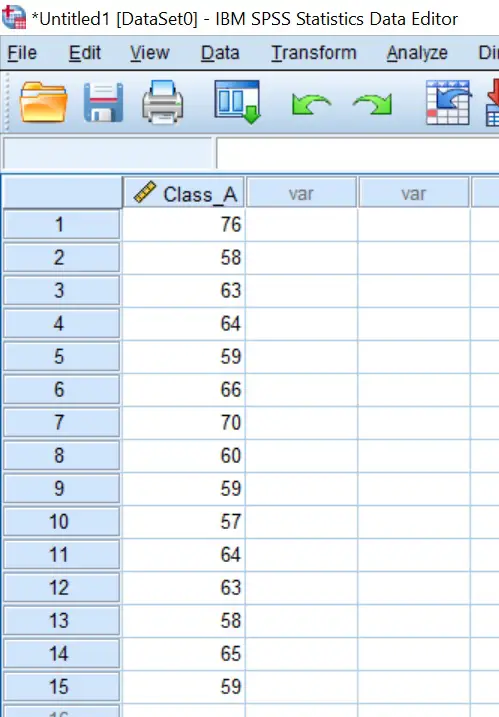
Before performing the one-sample t-test, let’s look at an example dataset.
For instance, say we have collected cognitive test scores from a sample of students in Class A. The scores are marked from 0 to 100. We want to know if the scores on this test differ from the average score gained in the country. The average national score on this test is 58. To do this comparison, a one-sample t-test will be used.
The null hypothesis would read:
There is no difference in scores on the cognitive test from students in Class A and the national average score.
The alternative hypothesis would be:
There is a difference in scores on the cognitive test from students in Class A and the national average score.
In SPSS I have just one dataset: Class A test scores. The test scores variable is simply called Class_A.
Performing a one-sample t-test in SPSS
Now, let’s perform the one-sample t-test in SPSS:
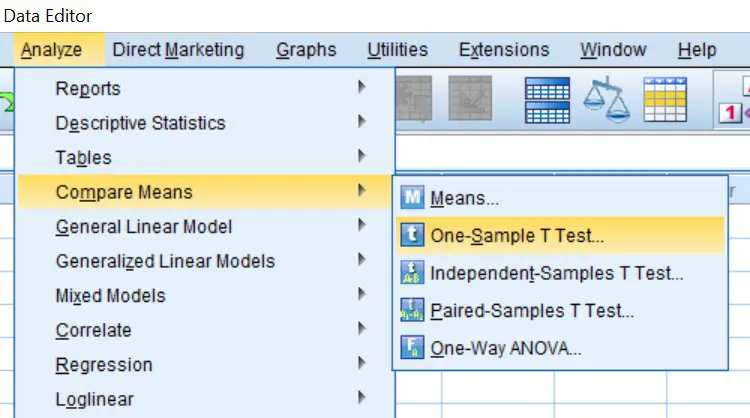
- Firstly, go to
Analyze > Compare Means > One-Sample T-Test....
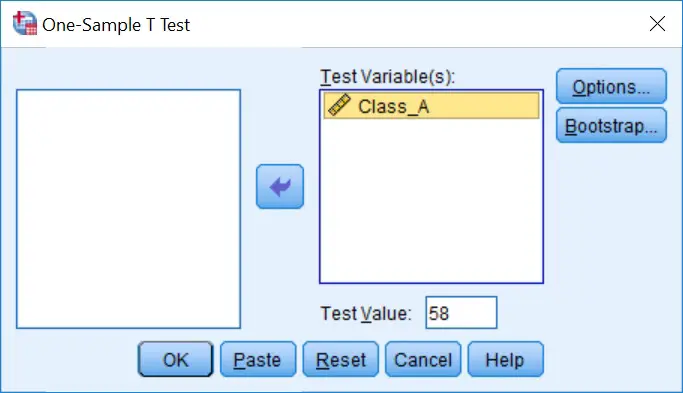
2. A new window will open. The variables which are to be included in the test need to be moved into the Test Variable(s) window. More than one variable can be entered at the same time.
Next, enter the value to be compared against in the Test Value box. In our example, this will be 58.
3. To run the test, click the OK button.
Output
Go to the output window in SPSS to view the results. You should see two boxes under the title T-Test:
The first box gives some descriptive statistics of the variables in the analysis. There are four columns presented:
N– The number of samples in the group.Mean– The average value of the group.Std. Deviation– The standard deviation of the group.Std. Error Mean– The standard error of the mean.
The results of the one-sample t-test are presented in the box below. At the top of the table, the Test Value is quoted. This was the value compared against. Under this, the table has six columns.
t– The t statistic.df– The number of degrees of freedom.Sig. (2-tailed)– The significance (P) value for the test in a two-tailed analysis.Mean difference– The difference between the group and tested value average.Lower (95% confidence interval of the difference)– The lower 95% confidence interval (CI) of the difference between the group and tested value.Upper (95% confidence interval of the difference)– The upper 95% CI of the difference between the group and tested value.
Interpretation
To determine if there is a significant result in the one-sample t-test, the Sig. (2-tailed) value should be examined. In this example, a value of 0.003 is reported. Since this value is less than our desired significance threshold (P<0.05), we reject the null hypothesis and accept the alternative hypothesis. In other words, the Class A results on this test are significantly different from that of the national average.
Reporting
To report the results of the test, it is useful to provide the t statistic, degrees of freedom and P value at the end of the sentence. For example, we could write:
IBM SPSS version used: 24






how to find test value?
Hi Adleehaqeem,
Many thanks for your message.
So do you mean the T statistic? In the output, this is found under ‘t’ in the table.
Thanks,
Steven