How To Perform A Non-Parametric Partial Correlation In SPSS

Partial correlations are great in that you can perform a correlation between two continuous variables whilst controlling for various confounders. However, the partial correlation option in SPSS is defaulted to performing a Pearson’s partial correlation which assumes normality of the two variables of interest.

But what if you want to perform a Spearman’s partial correlation on non-normally distributed data?

If you go to Analyze > Correlate > Partial … you will see that there is no option to select a Spearman correlation. There is, however, a way around this using a little coding.

In this guide, I will explain how to perform a non-parametric, partial correlation in SPSS.

The required dataset

To be able to conduct a Spearman partial correlation in SPSS, you need a dataset, of course. For our example, we have the age and weight of 20 volunteers, as well as gender. What we want to test is if there is a correlation between age and weight, after controlling for gender.

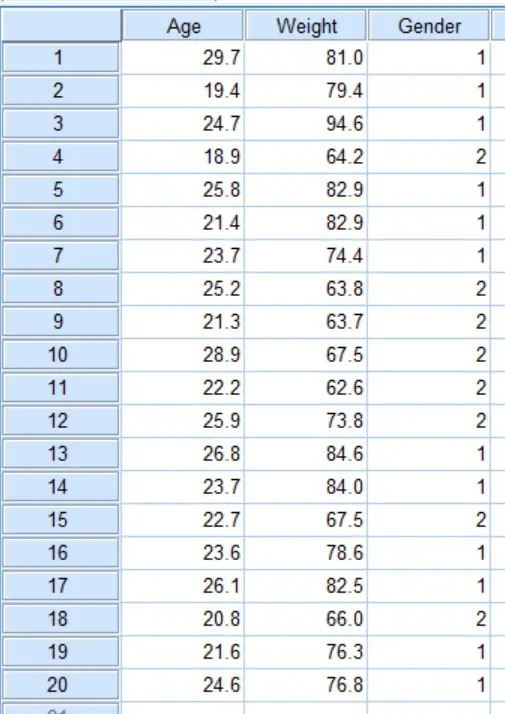Non-parametric partial correlation example data in SPSSCreating the script

For this to work, you need to enter a small piece of script into the SPSS Syntax Editor. Open up the Syntax Editor by going to File > New > Syntax.

Next, copy and paste the following code:

NONPAR CORR
/MISSING = LISTWISE
/MATRIX OUT(*).
RECODE rowtype_ ('RHO'='CORR') .
PARTIAL CORR
/significance = twotail
/MISSING = LISTWISE
/MATRIX IN(*).

You now need to add the appropriate variables next to the NONPAR CORR and PARTIAL CORR sections.

So, next to the NONPAR CORR enter all of the variables that will be involved in the partial correlation. In our example, this would be Age, Weight and Gender.

For the PARTIAL CORR line you need to enter the two variables of interest in the correlation followed by a BY then the variables you want to control for. Make sure all of the variables you enter match the ones in your file correctly, otherwise the script will fail.

Here is what our example will look like:

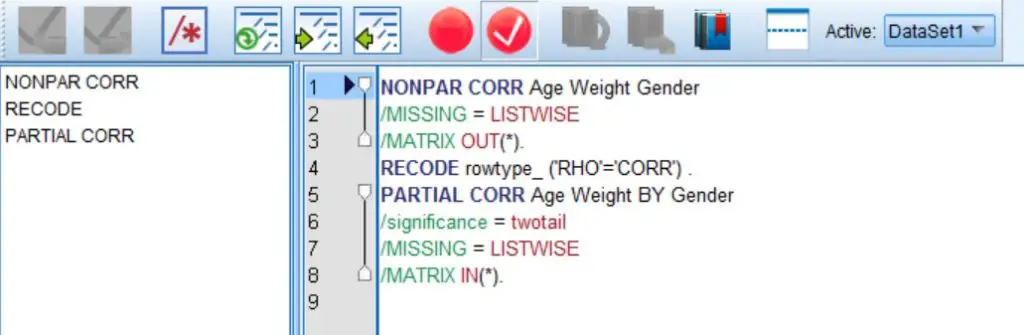
NONPAR CORR Age Weight Gender
/MISSING = LISTWISE
/MATRIX OUT(*).
RECODE rowtype_ ('RHO'='CORR') .
PARTIAL CORR Age Weight BY Gender
/significance = twotail
/MISSING = LISTWISE
/MATRIX IN(*).

And here is what it looks like in the Syntax Editor:

Non-parametric partial correlation syntax script in SPSSRunning the script

The script itself is separated into 3 parts: NONPAR CORR, RECODE and PARTIAL CORR.

The first is to perform a Spearman bivariate correlation for all variables and to add the Spearman rank correlation coefficients into a new file.

RECODE converts the row type from a Spearman (RHO) to a Pearson (CORR).

Finally, PARTIAL CORR performs the partial correlation on the desired variables by using the newly created Spearman correlation coefficients from the NONPAR CORR script.

Here is how to run the script:

1. To run the script, go to the Syntax Editor and with the NONPAR CORR section selected, hit the green play button.

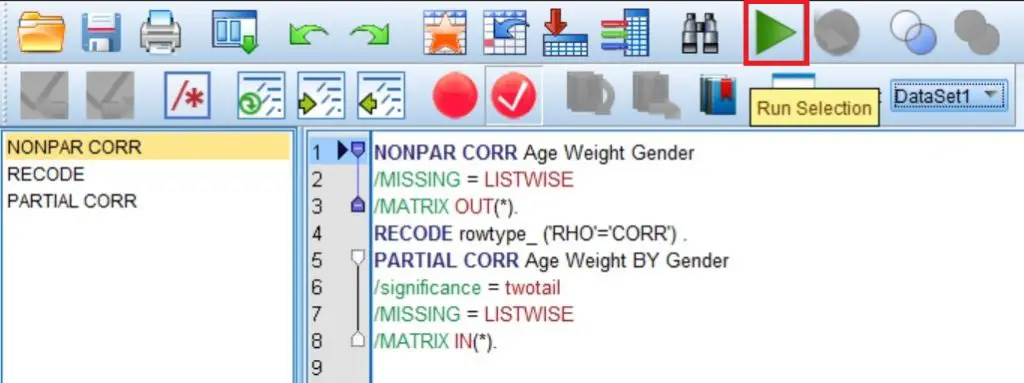Running the non-parametric partial correlation code in the syntax editor in SPSSThis will give you an output for the Spearman’s rho between the variables. If you go to the SPSS Output file you will see:

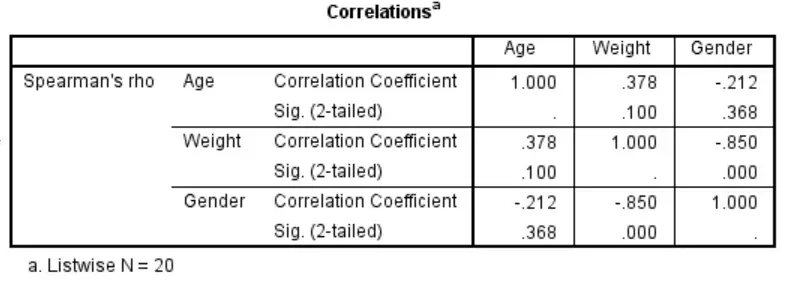Spearman correlation matrix in SPSSYou will also notice that a new SPSS data file has been created and is now open. This is usually named ‘Untitled’, or something similar. Within this file, you will see the Spearman’s rho values and n numbers for each correlation.

2. You next need to go back to the Syntax Editor window and run the RECODE part of the script. Make sure you select the new dataset as the active worksheet for this, as you want to perform the RECODE on the new sheet. You can toggle between datasets by clicking on the drop-down menu next to Active:. In this case, we select the Unnamed sheet:

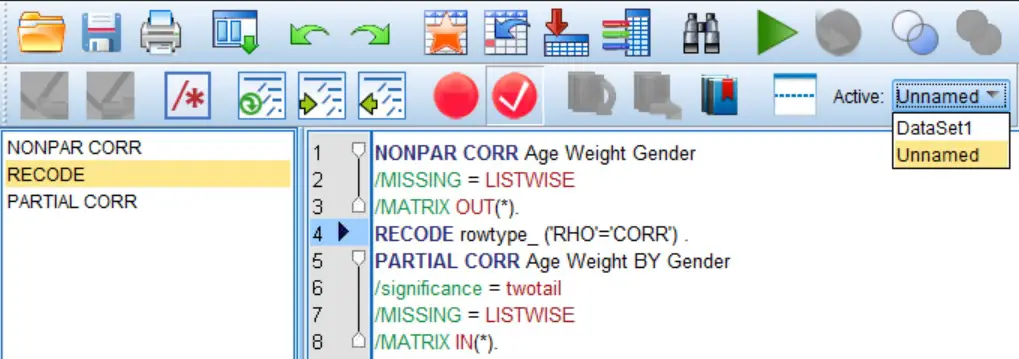Changing the active dataset in the syntax window of SPSSClick the green play button again to run the RECODE script on this.

3. Finally, still in the Syntax window, select the PARTIAL CORR code and run this on the same Unnamed dataset. This will perform the final partial correlation.

The output

By looking in the output file, you should now see a Partial Corr box which contains the partial correlation coefficients and P values for the test:

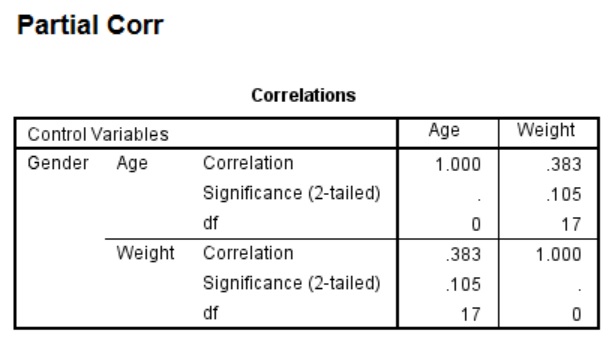Partial correlation matrix output in SPSSYou will see in this example that the non-parametric partial correlation for age with weight, after controlling for gender, has a coefficient value of ‘0.383’ and has a significant value of ‘0.105’.

Therefore, there is not a significant correlation for age and weight after accounting for gender.

RELATED ARTICLESMORE FROM AUTHOR

43 COMMENTS

  1. Hi Steven,

    Thank you so much for this guide. One quick question: when I run it, my degrees of freedom are off, which impacts my p values. I think my degrees of freedom are being based on the variables in the correlation matrix, not the actual number of cases. For example, although I have a sample size of 100, my df when I run the syntax ends up being 26. Although I am controlling for 6 variables and am not sure exactly what the df should be, 26 doesn’t seem right to me. From your screenshots, it doesn’t seem like you had this problem. Do you have any thoughts as to why this would happen? Thanks so much again!

    Emma

    • Hi Emma,
      So sorry for the delay.
      So do you have 100 cases and all of these have matching data for the variables being controlled for, ie there are no missing data points?
      Thanks,
      Steven

    • Hi Juan,
      I based this guide on the one produced by IBM. In that, they quote a reference:
      Conover, W.J. (1999), “Practical Nonparametric Statistics (3rd Ed.). New York: Wiley, (p. 327-328).
      This may be a good place to start?
      I hope that helps,
      Best wishes,
      Steven

  3. Hi Steven

    I’m using the SAS instead.

    Obtained from: https://en.wikipedia.org/wiki/Partial_regression_plot

    1) Computing the residuals of regressing the response variable against the independent variables but
    omitting Xi
    2) Computing the residuals from regressing Xi against the remaining independent variables
    3) Plotting the residuals from (1) against the residuals from (2).

    Example of SAS code: (I wish to acknowledge the contribution of Mr. Lin (Robbin@TMU), for his assistance in the longitudinal stats class)
    —
    SAS code:

    proc import datafile=”C:\Users\User\Desktop\working.xls” out=ddd replace dbms=excel;
    run;
    proc print;run;quit;

    *1. Computing the residuals of regressing the response variable against the independent variables but omitting Xi;
    proc reg data=ddd;
    model var1=ctrl1 ctrl2;
    output out=out1 residual=r1;
    run;
    proc print data=out1;run;quit;

    *2.Computing the residuals from regressing Xi against the remaining independent variables;
    proc reg data=ddd;
    model var2=crtl1 ctrl2;
    output out=out2 residual=r2;
    run;
    proc print data=out2;run;quit;
    *3.Plotting the residuals from (1) against the residuals from (2).;
    data out1 ;set out1; _n+1;run;
    data out2;set out2;_n+1;run;
    data out3;merge out1 out2; by _n;run;
    proc sgplot data=out3;
    scatter x=r1 y=r2;
    run;
    —
    Cheers
    Larry

  4. Hi Steven

    This is the SPSS syntax for the non-parametric partial corr the syntax example from SPSS forum (https://developer.ibm.com/answers/questions/223269/plotting-a-partial-corr-using-pairwise-exclusion/).

    The SPSS syntax as follows:
    —
    * Encoding: UTF-8.
    NONPAR CORR var1 var2 ctrlvar1 ctrlvar2
    /MISSING = LISTWISE
    /MATRIX OUT(*).
    RECODE rowtype_ (‘RHO’=’CORR’) .
    PARTIAL CORR var1 var2 BY ctrlvar1 ctrlvar2
    /significance = twotail
    /MISSING = LISTWISE
    /MATRIX IN(*).

    REGRESSION
    /MISSING LISTWISE
    /STATISTICS COEFF OUTS R ANOVA
    /CRITERIA=PIN(.05) POUT(.10)
    /NOORIGIN
    /DEPENDENT var1
    /METHOD=ENTER ctrlvar1 ctrlvar2
    /SAVE ZRESID.

    REGRESSION
    /MISSING LISTWISE
    /STATISTICS COEFF OUTS R ANOVA
    /CRITERIA=PIN(.05) POUT(.10)
    /NOORIGIN
    /DEPENDENT var2
    /METHOD=ENTER ctrlvar1 ctrlvar2
    /SAVE ZRESID.

    GRAPH
    /SCATTERPLOT(BIVAR)=RES_1 WITH RES_2
    /MISSING=LISTWISE.
    —
    Please feel free to comment on this syntax. Much obliged.

    Best wishes
    Larry Lai

    • Hi Larry,
      Thanks for sharing. Did this work for you? The syntax looks like it is doing a regression, similar to how I described, and plotting the residuals this way.
      Best wishes,
      Steven

  5. Hi Steven

    Thanks for sharing. By the way, how to plot a Non-Parametric Partial Correlation In SPSS?

    Thanks for considering my request.

    Cheers
    Larry

    • Hi Larry,
      Thanks for your comment!
      Plotting the results is something I have found quite difficult myself. But I am yet to find a conclusive answer.
      I have seen others which plot the results via a regression:
      What you can do in SPSS is plot these through a linear regression. Go to: Analyze -> Regression -> Linear Regression Put one of the variables of interest in the Dependent window and the other in the block below, along with any covariates you wish to control for. Then click the Plots button and tick the option for ‘Produce all partial plots’. Then run the test. One of the graphs produced will be the graph you are after. Hope that helps!
      Whether this is the correct way, however, I am not so sure – sorry.
      If you do find out, please come back and share!
      Best wishes,
      Steven

  6. Hi Steven,
    Thank you for this useful guide!
    I worked with this syntax but I get this warning:
    “The MATRIX subcommand on the PARTIAL CORR command specifies an input file which does not contain a correlation matrix for the current splitfile group. Within cell matrices are not acceptable. A correlation matrix has a row type of “CORR”.”

    can you help me out ?
    regards,
    Ferehsteh

  7. Unfortunately, one can not meaningfully apply the partial correlation formulas from parametric (usually Pearson’s) correlation to Spearman’s Rank correlation. You can apply the formulas as you have above, but the formulas were not developed for Spearman’s and the answers you get back are not meaningful partial correlations as they are with Pearson’s, so the Spearman’s the partial correlations are meaningless and can not be interpreted. This might not stop people doing it, but their resulting conclusions are fatally flawed.

    However, you can use Kendall’s Tau correlation for nonparametric correlation, and apply the same parametric partial correlation formula to get meaningful answers. Be aware though that Kendall’s Tau has a different meaning to Pearson’s r in explaining the correlation relationship. Unfortunately, there’s no easy way to apply significance testing to partial correlations based upon Kendall’s Tau since the underlying sample distribution is not defined (as it is for Pearson’s).

    So if you want partial correlations for nonparametric data, use Kendall’s Tau rather than Sprearman’s r.

  8. Hello! Thanks for this wonderful guide. Do you have any suggestions for how to plot the results of the nonparametric partial correlation on a graph? I cannot figure this out or find anything online.

  10. Thank you so much for a very helpful post and also helpful comments and replys above.
    Is it possible to enter more than two variables at the same time (before BY)? Or do I have to repeat it for every depending variable I want to test?

    • Hello Ingrid,
      Many thanks for your comments and kind words. I presume you can enter more than 2 variables before the ‘BY’. The results should then display a grid table so you can look at all your correlations within the same output.
      Let me know if there is an issue with this however.
      Thanks!
      Steven

      • Thank you for the reply. It worked and gave a grid table as you said. If you want to test the correlation between one (undepenent) variable and all the others (depentend) varaibles, you can place that one first or last and write WITH between in the partial recode.

        Example: PARTIAL CORR Age WITH Weight Pain BY Gender
        Then the output will show only Age as a horisontal collum and Weight and Pain in the vertical collums.

  12. Hi Steven,

    I am running your script, but having an error below. The problem is the new “unnamed” or “unknown” data sheet does not exist or I can’t find it. What to do?

    Thanks,

    Terhi

    DATASET ACTIVATE DataSet1.
    RECODE ROWTYPE_ (‘RHO’=’CORR’).

    Error # 4631 in column 8. Text: ROWTYPE_
    On the RECODE command, the list of variables to be recoded includes the name
    of a nonexistent variable.
    Execution of this command stops.

    • Hello Terhi,
      So sorry for the late reply. Did you manage to sort this? It seems like the new results are not being opened in a new datasheet. Have you ensured the ‘/MATRIX OUT(*).’ part of the code is included before you run the RECODE part of the code.
      Thanks
      Steven

  13. Hi Steve,

    Great post. Do you know how to compute 95% confidence intervals for Spearman’s partial correlations using the syntax? My reviewers are requesting confidence intervals for all point-estimates in accordance with APA.

    Thanks,

    Rose

    • Hi Rose,

      Thanks for the comment. Unfortunately I do not know how to report 95% CI for this. Upon reading around this it seems quite a few people are asking the same thing. I have found a link to this website however, http://vassarstats.net/rho.html, which computes 95% CI from the r and n values. May be of use for you?

      Thanks,

      Steven

    • Hi Rose:

      This reply may have come a little late for you. As I posted below, there is no such thing as partial correlations for Spearman’s rho. Therefore, compute Kendall’s Tau, where you can calculate meaningful partial correlations. However, even for Kendall’s Tau, there is no defined sampling distribution, and so CIs can not be calculated. You can move forward in a few ways: First carefully review your data to be sure that Pearson’s r can not be used. Pearson’s r is pretty robust, and unless your data are very skewed from normal, you might be able to proceed (don’t get distracted by the type of data you collecting, you can apply Pearson’s r even to categorical data). If the first approach does not work, try a data transformation to make your data sufficiently normal to apply Pearson’s r (Spearman’s itself is a kind of rank data transformation). Finally, if you end up using Kendall’s Tau you might be able to apply bootstrap methods to develop a sampling distribution to create CIs around the partial correlations. This is a last resort for most people, and I’ve rarely seen this done.

      Ian

  14. Hi, Steven
    Thank you so much for providing this. I read the IBM instructions for syntax and was totally bamboozled; your tutorial and example was very easy to follow and was immensely helpful!
    FYI, I am using SPSS V24 on a Mac. When I ran the second part of the syntax [RECODE rowtype_ (‘RHO’=’CORR’) .] I received a warning message. I removed the space between “rowtype_” and “(‘rho’=’corr’) and re-ran without any further problems [ie. RECODE rowtype_(‘RHO’=’CORR’) .].
    regards
    Marie

    • Hi Marie,

      Thanks very much for the feedback, very much appreciated. Also, thanks for providing details for the Mac users. Unfortunately I am just on Windows at the minute so I cannot provide too much information on that system, but maybe in the future I can expand :).

      Best wishes,

      Steven

    • Hi,
      I’m on a Mac also and I found the warning message disappeared if I ensured I had clicked at the top of the syntax (so that the procedure was run from the right place and not halfway down the command).

      • Hi Rose,
        Thanks very much for this, I was having exactly the same problems as you (on a Mac) and found that clicking the top of the syntax sorted this. Your info sharing and advice has made a happy student!

    • Hi Omar,

      Thanks for the feedback. Yes, you can control for more than one variable. However, the more variables you are controlling for the less reliable the test may become because you may over-fit your analysis. If you have a large enough sample size then it should be okay. One rule, called the One in Ten rule (https://en.wikipedia.org/wiki/One_in_ten_rule), is suggested for regression analysis and could be kept in mind when doing a partial correlation. Briefly, for every control (or predictor) variable you use there must be at least 10 samples in the analysis.

      Hope that helps!

        • When more than one control variable is entered then only one ‘BY’ is required. So:

          Age Weight BY Gender SES Ethnicity

          This will control for ‘Gender’, ‘SES’, and ‘Ethnicity’.
          Hope that helps 🙂

  16. Also, are you sure partial correlations can be run by categorical variable? I thought it was only to control for a continuous variable.

  17. Hey Steven,

    I am trying to run your syntax, but my output says:
    “The input matrix file does not contain a ROWTYPE_ variable or the variable has been misspecified.”
    Could you help me out?
    Thank you!

    • Hi Jess,

      Sorry for the late response. The error you are getting, when do you get this? Is this for the first (nonpar corr), second (recode) or third (partial corr) part of the script?

      Thanks!

      • Hi Steven,

        I am also experiencing this error. I get it at the second [RECODE rowtype_ (‘RHO’=’CORR’)] part of the script.

        The exact error message is as Jess stated, “The input matrix file does not contain a ROWTYPE_ variable or the variable has been misspecified.”

        Thanks in advance

        • Hi Lauren,

          I think this error is because you may be running the RECODE part of the script using original datasheet. Have you changed the ‘Active’ sheet to the newly created ‘unnamed’ one before running the RECODE part? (See point 2 in the guide above).

          I am in the process of creating a screencast video that will hopefully help.

          Let me know if this works 🙂

          Thanks

LEAVE A REPLY

Please enter your comment!
Please enter your name here