This guide will explain, step by step, how to perform a one-way ANOVA test in the SPSS statistical software by using an example. The guide will also explain how to perform post-hoc tests to investigate significant results further.
What is a one-way ANOVA test?
A one-way analysis of variance (ANOVA) test is a statistical tool to determine if there are any differences between the means of three or more continuous variables. This particular test assumes that the data in each group is normally distributed.
Assumptions of a One-Way ANOVA test
Before running a One-Way ANOVA test in SPSS, it is best to ensure the data meets the following assumptions.
- The dependent variables should be measured on a continuous scale (either interval or ratio).
- There should be three or more independent (non-related) groups.
- There are no outliers present in the dependent variable.
- The dependent variables should be normally distributed. See how to test for normality in SPSS.
- The dependent variables should have homogeneity of variances. In other words, their standard deviations need to be approximately the same.
Example experiment
I will use an example to explain how to perform a one-way ANOVA test. For instance, say we have measured the weights of different rats. There are three groups of rats:
- Controls: these have not received any physical exercise.
- Exercised: these have performed 6 weeks of physical exercise.
- Pill: these have been treated with a diet pill for 6 weeks.
We want to know if there are any differences between the weights of the rats after the 6 week period. We can now formulate two hypotheses.
The null hypothesis would read:
There is no differences in the weights of the rats after the 6 week period.
The alternative hypothesis would be:
There is a difference in weight between the three rat groups.
The one-way ANOVA test will be able to inform us if there is a significant difference between the three groups. However, it cannot directly state which group(s) are different from each other. So, if a one-way ANOVA test indiciates a significant result, further post-hoc testing is required to investigate specifically which groups are significantly different.
The dataset
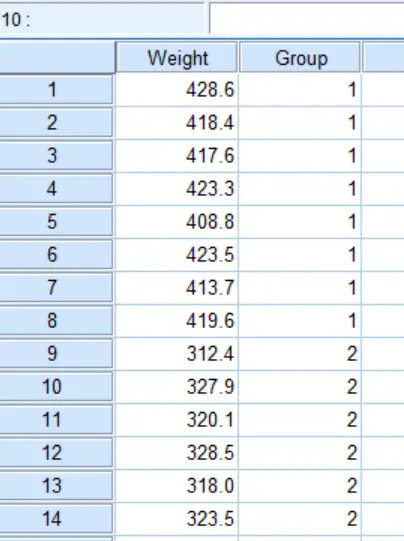
In SPSS, I have created a file containing two data variables labelled ‘Weight’ and ‘Group‘. The first contains all of the rat weights (measured in grams). In the ‘Group‘ column, I have assigned the numbers ‘1‘, ‘2‘, or ‘3‘ to indicate which experiment group the rats belong to.
Below is a snapshot of what part of the data looks like so you get the idea.
 Performing a One-Way ANOVA test in SPSS
Performing a One-Way ANOVA test in SPSS
Now we have the dataset, let’s perform the one-way ANOVA test in SPSS.
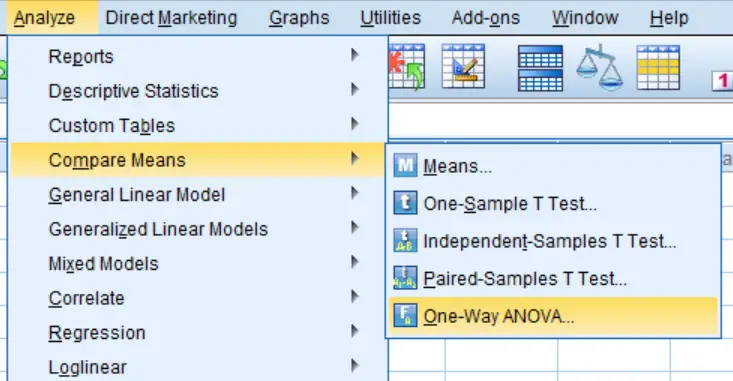
1. Firstly, go to Analyze > Compare Means > One-Way ANOVA....
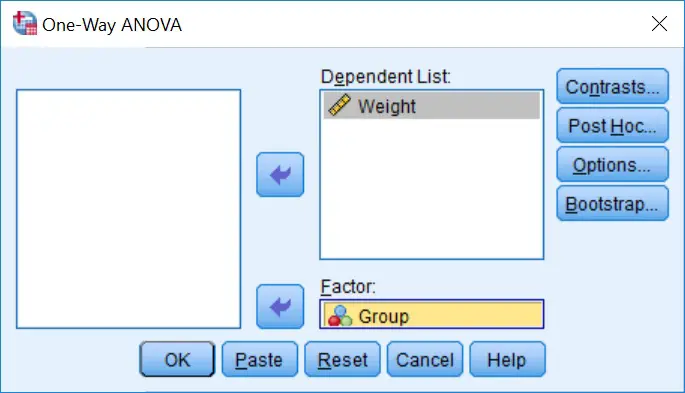
2. A new window will open. Here you need to move the depdendent variable (Weight in the example) into the window called Dependent List and the grouping variable (Group) into the box titled Factor.
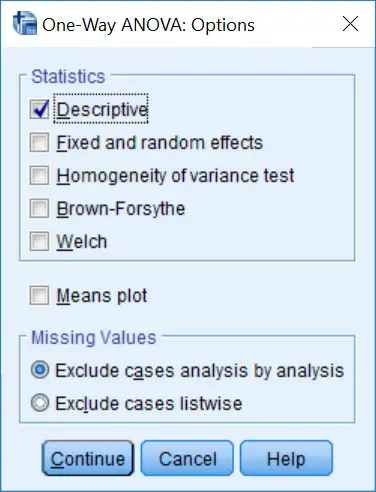
 3. Since we do not know whether there are any differences in weights between our three groups, we should avoid performing any post-hoc test just yet. It is, however, worth getting further descriptive data at this point. To do this, click the
3. Since we do not know whether there are any differences in weights between our three groups, we should avoid performing any post-hoc test just yet. It is, however, worth getting further descriptive data at this point. To do this, click the Options... button. This will bring up a new window, here you should tick the Descriptive option under the Statistics heading and click the Continue button.
 4. Finally, click the
4. Finally, click the OK button to run the ANOVA test.
One-way ANOVA Output
The results are presented in the output window in SPSS. You should be presented with two boxes.
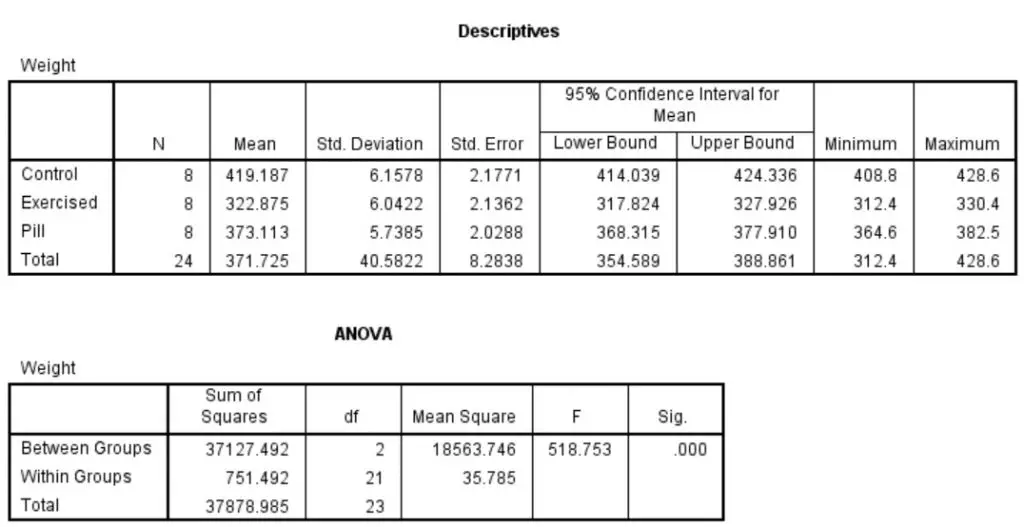 The first (
The first (Descriptives) contains a wealth of information including mean, standard deviation, standard error and 95% confidence intervals stratified by each group, as well as combined. We can clearly see large differences in mean weight values.
The next output box (ANOVA) contains all of the statistical information regarding the one-way ANOVA test. This includes the degrees of freedom (df), the F statistic (F) and the all important significance value (Sig.).
One-Way ANOVA interpretation
By looking at the table we can see that the significance (Sig.) value is ‘.000‘. This is considerably lower than our significance threshold of P<0.05. Therefore, we should reject the null hypothesis and accept the alternative hypothesis.
One-Way ANOVA reporting
At this point, we can confirm that there is a significant difference in rat weights between the three groups. Thus we could summarise this, including the statistical output, in one simple sentence.
The reporting includes the degrees of freedom, both between and within groups, the F statistic and the P value.
Performing post-hoc tests
Since the results of the one-way ANOVA test returned a significant result, it is now appropriate to carry out post-hoc tests. This is to determine which specific groups are significant from another.
- To perform post-hoc tests in SPSS, firstly go back to the one-way ANOVA window by going to
Analyze > Compare Means > One-Way ANOVA...(as described in Step 1). - Now, enter the same data into the appropriate windows again (as described in Step 2).
- Click the
Post Hoc...button to open thePost Hoc Multiple Comparisonswindow. There are multiple options for post hoc testing, but for this example we will use the commonly adopted Tukey post hoc test. Tick theTukeyoption under theEqual Variances Assumedheading.
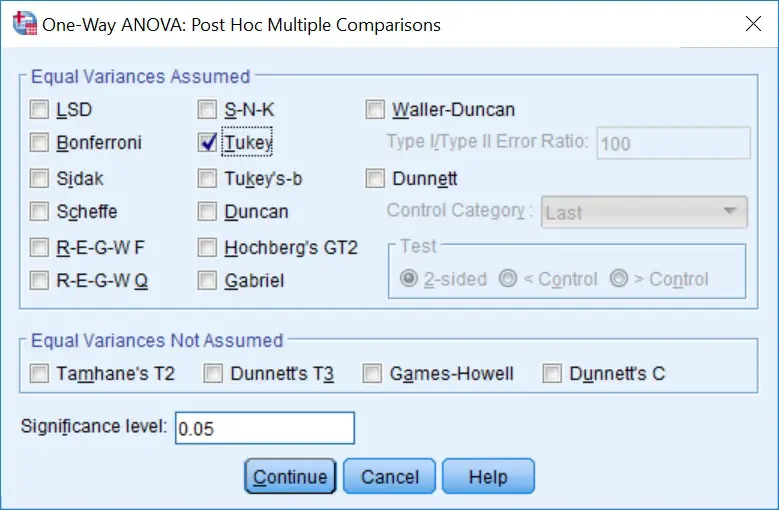 Now click the
Now click the Continue button.
4. To run the test, click the OK button.
Post-hoc (Tukey) output
By going to the output window, you will now see a new section of results titled Post Hoc Tests. The results that we are interested in are presented in the Multiple Comparisons box.
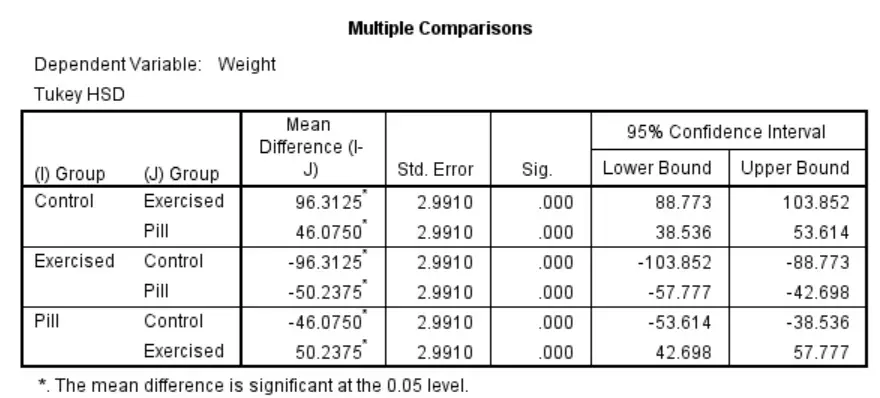 The output compares each possible group. For example, the first row presents the results for the comparison between the ‘Control‘ and the ‘Exercised‘ groups, as well as that between the ‘Control‘ and ‘Pill‘ groups. The
The output compares each possible group. For example, the first row presents the results for the comparison between the ‘Control‘ and the ‘Exercised‘ groups, as well as that between the ‘Control‘ and ‘Pill‘ groups. The Mean Difference is also given, which is the average difference in weights between the groups in comparison. Additionally, the table contains the standard error (Std. Error) and 95% confidence intervals. The P values for each comparison can be found under the Sig. column.
Post hoc (Tukey) interpretation
By looking at the Sig. column, it can be seen that all comparisons are significant since the P values are all .000. Thus, the weights for the three rat groups are significantly different from each other.
Post hoc (Tukey) reporting
Since we now know the comparisons between each group, we can add to our previous reporting with the additional post-hoc results. I have provided an example for the full reporting below.
IBM SPSS version used: 23






Dear Dr. Steven
I really like your Website that explain everything clearly . I would be most grateful if you can send or post How To Perform A Two -Way ANOVA Test In SPSS
Thank you so much.it was easy to understand and helpful
ITS VERY IMPRESIVE. KEEP IT UP
Thanks so much , I have found it so valuable.
Excellent lectures to under stand and use SPSS .
Please can you explain us that how to make data sheet in spss before anova
Hi Nidhi,
Many thanks for your comment.
Of course, I can write an article for this and let you know once it is up and running.
Thanks,
Steven